Chapter 9
CuTe-MCFM

9.1 N${}^3$LL and N${}^4$LL $q_T^2$ resummation for color-singlet processes in MCFM

Based on arXiv:2009.11437 (Becher, Neumann ’20).

The $q_T$ resummation in CuTe-MCFM is available for color-singlet processes and based on a factorization theorem in SCET. It is fully differential in the Born kinematics and matches to large-$q_T^2$ fixed-order predictions at relative order ${\alpha }_s^2$. It provides an efficient way to estimate uncertainties from fixed-order truncation, resummation, and parton distribution functions. In addition to $W,Z$ and $H$ production, also the diboson processes $\mathit{\gamma \gamma }$, $\mathit{Z\gamma }$, $\mathit{ZH}$, $\mathit{WH}$, $\mathit{WW}$, $\mathit{WZ}$ and $\mathit{ZZ}$ are available, including decays.

While CuTe-MCFM can calculate $q_T$-resummed results without using pregenerated beam functions grids, we recommend that LHAPDF grid files are generated for the beam functions beforehand for a choice of a PDF set. This significantly accelerates the evaluation of the beam functions and the integration.

CuTe-MCFM ships with pregenerated beamfunction grids for the central values of CT14nnlo and NNPDF31_nnlo_as_0118, which are included in the Bin/PDFs directory. This path is automatically used as the preferred path for LHAPDF grid files. With these pregenerated grids the example input files work out of the box. For other PDF sets or when using PDF errors, the first run of CuTe-MCFM should be with the setting makegrid=.true.. Additionally the input and output directories for the PDF grids have to be specified. For example the input directory is typically /usr/local/share/LHAPDF/ (or the PDFs/ directory relative to the mcfm executable in Bin) and the output directory should be a user-writeable directory like /home/user/gridout/ (or PDFs/). Note the trailing slashes.

When calling mcfm with makegrid=.true. only the beam function grids are written during that run, and mcfm exits afterwards. We recommend to use PDFs/ as the gridout path, since this path is automatically added to the LHAPDF search paths, and you won’t have to copy the generated grid directories to your LHAPDF grid directory or set the LHAPDF_DATA_PATH environment variable to the gridout path.

For example for the set CT14nnlo the grid directories CT14nnlo_B00, CT14nnlo_B10, CT14nnlo_B11, CT14nnlo_B20, CT14nnlo_B21, CT14nnlo_B22 and CT14nnlo_G10 are written and have to be copied to the directory where LHAPDF searches for the grid files. When the gridout path is chosen as PDFs/ no further action is necessary. The LHAPDF grid file search path can be modified by setting the shell environment variable LHAPDF_DATA_PATH to the desired directory, but the PDFs directory is always used as the preferred directory.

The next run of mcfm should be done with makegrid=.false. and usegrid=.true..

Other important parameters for the resummation are res_range, determining the integration range of the purely resummed part, resexp_range, determining the integration range of the fixed-order expanded resummed part, and fo_cutoff which sets the lower $q_T$ cutoff for the fixed-order part. Typically this cutoff should agree with the lower range of resexp_range. For example for $Z$ production one can integrate up to $m_Z$ with a cutoff of 1 GeV: res_range = 0.0 90.0, resexp_range = 1.0 90.0, qt_cutoff = 1.0.

For details regarding these parameters see the next section. The transition function is also discussed below.

9.2 Input file parameters

The [resummation] section has been added to the input file to control the resummation. The following keys are available:

We strongly recommend to calculate resummed results with pregenerated grids, see the previous section. The integration range for the purely resummed part can be controlled with the key res_range and should typically be between $0$ and some upper value. For example for $W^{\text{±}},Z$ or $H$ production this can just be the boson mass. For other processes there can be thresholds and this number must be selected more carefully to not run into numerical issues, see arXiv:2009.11437.

The setting resexp_range and fo_cutoff are relevant for the matching corrections. The values of the resexp_range determine the integration range for the fixed-order expansion of the resummed part. The minimum should typically be at least one GeV for numerical stability. For smaller values significantly more time goes into the integration, and the minimum number of Vegas calls might need to increased. For single boson processes the maximum value can again be the boson mass, although it can be set to a value where the implemented transition function fully switches to zero. The fixed-order cutoff fo_cutoff determines the minimum $q_T$ for the fixed-order calculation. This should typically agree with the lower range of the resexp_range.

Lastly, the parameter transitionswitch is passed for convenience to the plotting routines where the transition function is implemented. It can be used for for an easy control of the transition region as described in the following.

9.3 Plotting routine and transition function

The following transition function is implemented for the example input files. For more details we refer to our publication. The fully matched cross-section is described in general by

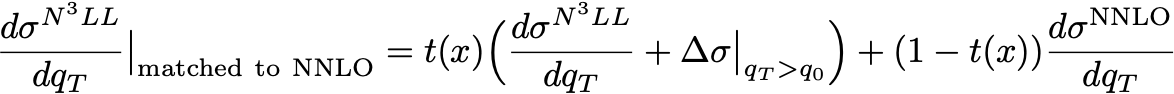
using a transition function $t(x)$. We have implemented a transition function $t$ with $x=q_T^2∕Q^2$ that smoothly switches between 1 and 0 like a sigmoid function.

Following a choice in CuTe, we first define

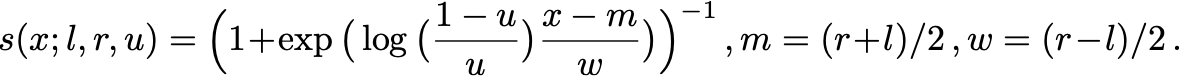
The function $s(x)$, parametrized by $l,r,u$, is defined to be $s(l)=1-u$ and $s(r)=u$. In terms of this sigmoid, our transition function $t(x;x^{\text{min}},x^{\text{max}},u)$, where $x=q_T^2∕Q^2$, is then defined by

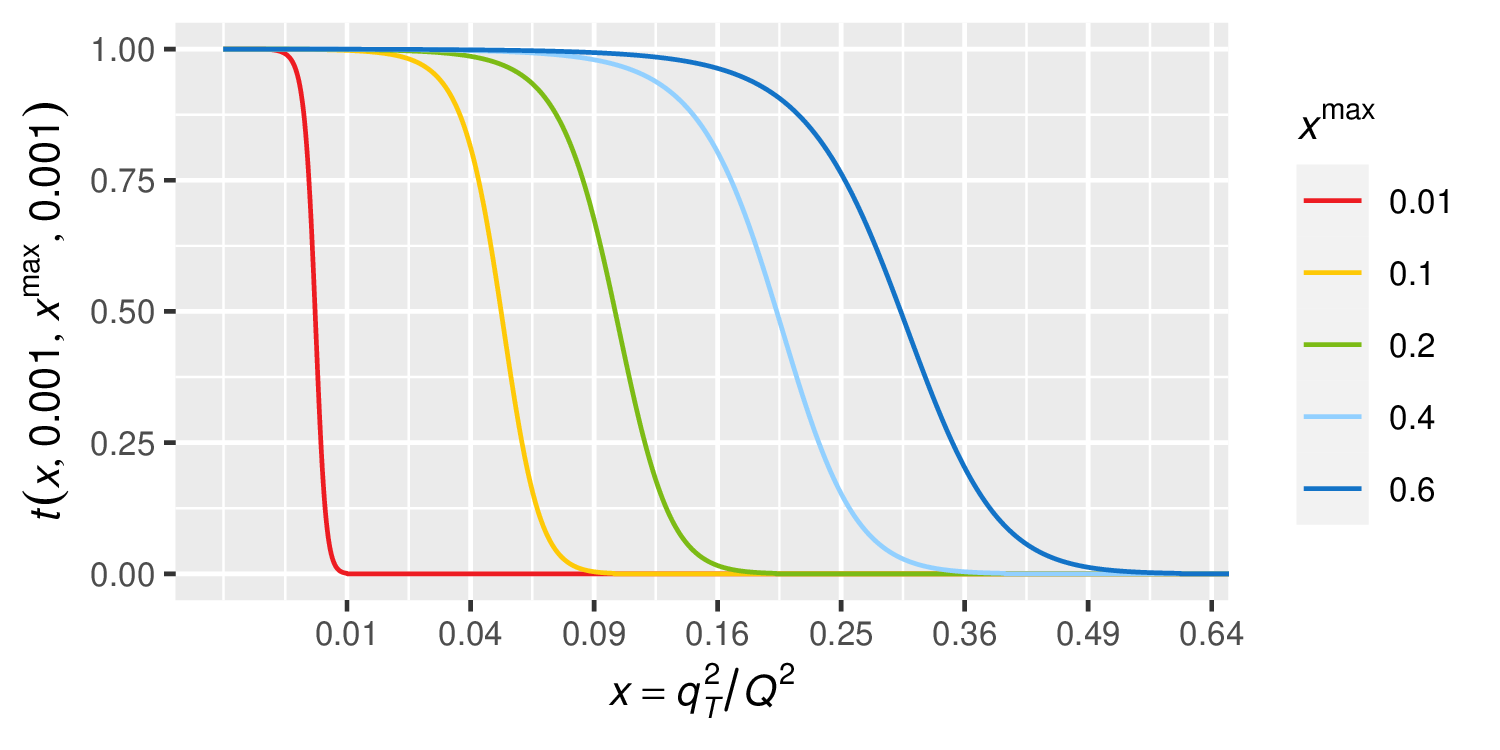
This ensures that below $x^{\text{min}}={(q_T^{\text{min}}∕Q)}^2$ only the naively matched result is used, and at $x^{\text{max}}$ for small $u\ll 1$ the transition function is approximately $u$. In practice it makes sense to set the transition function to zero below a small threshold like $10^{-3}$ without a noticeable discontinuity. This has the advantage that the deteriorating resummation and matching corrections do not impact the region of large $q_T$ at all. Our example plotting routines use $x^{\text{min}}=0.001$, and $u=0.001$, and the parameter $x^{\text{max}}$ corresponds to the value of transitionswitch set in the input file. The transition function can be changed or completely replaced by just modifying the plotting routines. The following figure illustrates this transition function.

9.4 Modifying the plotting routines and transition function.

The plotting infrastructure has been completely rewritten for CuTe-MCFM, and we recommended to only use the new infrastructure from this point on by setting histogram%newstyle = .true. in the input file. This is the default for the CuTe-MCFM example input files.

For the processes $W^{\text{±}},Z,H$, $\mathit{\gamma \gamma }$, $\mathit{Z\gamma }$, $\mathit{ZH}$ and $W^{\text{±}}H$ we include predefined plotting routines that can be adjusted. For example for $Z$ production the plotting routine is in the file src/User/nplotter_Z_new.f90, and similarly for the other processes. The routine setup defines all histograms with custom or uniform binning and names. The number of used histograms needs to be allocated in this routine. The routine book is called for each phase space point. Through the boolean variable abovecut it is known whether the routine is called for “boosted $q_T=0$” (resummed part and fixed-order expansion of resummed part) or for $q_T>0$ (fixed-order). All provided example input files use the transition function as defined above, see also arXiv:2009.11437.

The plotting routine returns the calculated observables in the vals array, and Vegas weights in wts. The transition function is implemented by reweighting the original Vegas weights with the output of the transition function. To disable the transition function, one sets trans to $1$ before filling the wts array.

Apart from modifying a default set of kinematical cuts in the input file, cuts can also be set in the file src/User/gencuts_user.f90 in a fully flexible way based on the event’s four momenta. Some commented out examples are included there.