Chapter 13
Notes on specific processes
The processes described in the file process.DAT include appropriate boson decays
when the parameter removebr is set to .false.. In many cases a more simple
calculation can be performed by setting this parameter to .true., in which case these
decays are not performed. Technically the full calculation including the decays is still
performed but cuts are not performed on the decay products and the branching
ratio is divided out, thus yielding the cross section before decay. In the notes below
we indicate the simpler processes thus obtained. When running in this mode, the
parameter zerowidth should be set to .true. for consistency. However in certain
circumstances, for the sake of comparison, it may be useful to run with it set to
.false..
13.1 -boson production, processes 1,6
These processes represent the production of a boson which subsequently decays leptonically. This process can be calculated at LO, NLO, and NNLO. NLO calculations can be performed by dipole subtraction, zero-jettiness slicing and -slicing. NNLO calculations can be performed by zero-jettiness slicing and -slicing.
When removebr is true, the boson does not decay.
13.2 EW corrections to -boson production, processes 2,7
These processes compute the electroweak corrections to the production of a boson which subsequently decays leptonically. The electron is taken to be massless. The electroweak corrections involve both real and virtual corrections. If particle 5 is present it is a photon. The calculation must be performed at NLO, i.e. part=nlo.
13.3 Photon-induced corrections to -boson production, processes 3,8
These processes compute the production of a boson, (which subsequently decays leptonically), through the reaction . The calculation must be performed at NLO. Since the reaction has an initial photon, it is important to have an accurate parton distribution function for the photon in the proton, e.g. LUXqed17_plus_PDF4LHC15_nnlo_30.
13.4 jet production, processes 11,16
This process is calculable at leading LO and next-to-leading order NLO. These processes represent the production of a boson which subsequently decays leptonically, in association with a single jet. When removebr is true, the boson does not decay.
13.5 production, processes 12,17
These processes represent the production of a boson which subsequently decays leptonically, in association with a single bottom quark, exploiting the weak transitions and . This is produced at leading order by an initial state which contains a charm quark (or the CKM suppressed quark) and a gluon, e.g and or the charge conjugate processes for . This process is somewhat analogous to single top production.
The effect of the bottom quark mass is included throughout the calculation. For this case the CKM matrix elements and , (if they are equal to zero in the input data file, mdata.f) are set equal to and respectively. Otherwise the non-zero values specified in mdata.f are used. The calculation of this process may be performed at LO and NLO.
When removebr is true, the boson does not decay.
13.6 production, processes 13,18
These processes represent the production of a boson which subsequently decays leptonically, in association with a charm quark. This is produced at leading order by an initial state which contains a strange anti-quark (or Cabibbo suppressed anti-quark) and a gluon, e.g and or the charge conjugate process for . This process is somewhat analogous to single top production.
The effect of the charm quark mass is included throughout the calculation. The calculation of this process may be performed both at LO and NLO.
When removebr is true, the boson does not decay.
13.7 production (), processes 14,19
These processes are identical to 13 and 18 except for the fact that the charm quark mass is neglected. The calculation can currently be performed at LO only.
13.8 production, processes 20,25
This process is calculable at leading LO and next-to-leading order NLO. These processes represent the production of a boson which subsequently decays leptonically, in association with a pair. The effect of the bottom quark mass is included throughout the calculation. This calculation may be performed at NLO, thanks to the incorporation of the virtual corrections from ref. [13]. When removebr is true, the boson does not decay.
To select final states in which one of the -quarks may be unobserved the user can employ processes 401-408 instead. These processes use the same matrix elements but make specific requirements on the kinematics of the -quarks and QCD radiation.
13.9 production (), processes 21,26
This process is calculable at leading LO and next-to-leading order NLO. These processes are identical to 20 and 25 except for the fact that the bottom quark mass is neglected. Processes nproc=20,25 with a massive -quark should be used in preference. However processes nproc=21,26 run considerably faster than the corresponding processes with the mass for the quark, (nproc=20,25). In circumstances where both quarks are at large transverse momentum, the inclusion of the mass for the -quark is not mandatory and a good estimate of the cross section may be obtained by using these processes.
When removebr is true, the boson does not decay.
13.10 jets production, processes 22,27
This process represents the production of a boson and jets, where the boson decays leptonically. The calculation may be performed up to NLO, as detailed below. Virtual amplitudes are taken from ref. [17]. For more details on this calculation, please see Refs. [15, 16].
For these processes (and also for jet production, nproc=44,46) the next-to-leading order matrix elements are particularly complex and may be divided into two groups. The division is according to the lowest order diagrams from which they originate:
- Diagrams involving two external quark lines and two external gluons, the “Gflag” contribution. The real diagrams in this case thus involve three external gluons.
- Diagrams where all four external lines are quarks, the “Qflag” contribution. The real diagrams in this case involve only one gluon.
By specifying Gflag and Qflag in the file input.ini one may select one of these options at a time. The full result may be obtained by straightforward addition of the two individual pieces, with no meaning attached to either piece separately. The default is that both of these are set to .true. simultaneously.
Virtual amplitudes are taken from ref. [17].
When removebr is true, the boson does not decay.
13.11 jets production, processes 23,28
This process represents the production of a boson and jets, where the boson decays leptonically. The calculation may be performed at LO only.
When removebr is true, the boson does not decay.
13.12 jet production (), processes 24,29
These processes represent the production of a boson which subsequently decays leptonically, in association with a pair and an additional jet. The effect of the bottom quark mass is neglected throughout and the calculation may be performed at LO only. The corresponding LO processes with a mass for the -quark are given given in nproc=431,436 and should be used in preference to these processes.
When removebr is true, the boson does not decay.
13.13 -boson production, processes 31–33
These processes represent the production of a boson which subsequently decays either into electrons (nproc=31), neutrinos (nproc=32) or bottom quarks (nproc=33). Where appropriate, the effect of a virtual photon is also included. As noted above, for nproc=31 and nproc=33 the constraint m34min > 0 is obligatory. The calculation may be performed at LO, NLO and NNLO [11, 21] although the NLO and NNLO calculation of process 33 does not include radiation from the bottom quarks (i.e. radiation occurs in the initial state only).
This process can be calculated at LO, NLO, and NNLO. NLO calculations can be performed by subtraction, zero-jettiness slicing and -slicing. NNLO calculations can be performed by zero-jettiness slicing and -slicing.
To calculate the total cross section to on-shell bosons, we take process (nproc=32), (no contribution) and set (zerowidth=.true.) and (removebr =.true.). When removebr is true in process 31, the boson does not decay.
13.14 -boson production decaying to jets, processes 34–35
Thes processes are calculable at leading LO and next-to-leading order NLO, nproc=34 gives and nproc=35 gives. Radiation from the final state quarks is not included in this process.
13.15 production mediated by -boson exchange, process 36
These processes represent the production of a virtual boson or photon which subsequently decays into . The leptonic decays of the top quarks are included. Switching zerowidth from .true. to .false. only affects the bosons from the top quark decay. Note that m34min > 0 is obligatory due to the inclusion of the virtual photon diagrams. The calculation may be only be performed at LO. This is a small contribution, but in -collisions gives a forward backward asymmetry.
13.16 Lepton pair production through photonic initial states, process 310
This process is calculable at leading order LO. This process represents the production of a lepton pair through an electroweak process involving two photons in the initial state, . Since the reaction has initial photons, it is important to have an accurate parton distribution function for the photon in the proton, e.g. LUXqed17_plus_PDF4LHC15_nnlo_30.
13.17 jet production, processes 41–43
These processes represent the production of a boson and a single jet, where the subsequently decays either into electrons (nproc=41), neutrinos (nproc=42) or bottom quarks (nproc=43). Where appropriate, the effect of a virtual photon is also included. The calculation may be performed at LO and NLO and NNLO[9] although the NLO, (NNLO) calculation of process 43 does not include radiation from the bottom quarks. The one-loop virtual amplitudes are taken from the appendix IV of ref. [17].
When removebr is true in process 41, the boson does not decay.
13.18 jets production, processes 44, 46
These processes represents the production of a boson and jets, including also the effect of a virtual photon (nproc=44 only). The decays to an pair (nproc=44) or into three species of neutrino (nproc=46). Virtual amplitudes are taken from ref. [17]. For more details on this calculation, please see Refs. [15, 16].
The calculation may be performed up to NLO. For jet production the next-to-leading order matrix elements are particularly complex and so they have been divided into two groups. The division is according to the lowest order diagrams from which they originate:
- Diagrams involving two external quark lines and two external gluons, the “Gflag” contribution. The real diagrams in this case thus involve three external gluons.
- Diagrams where all four external lines are quarks, the “Qflag” contribution. The real diagrams in this case involve only one gluon.
By specifying Gflag and Qflag in the file input.ini one may select one of these options at a time. The full result may be obtained by straightforward addition of the two individual pieces, with no meaning attached to either piece separately. The default is that both of these are set to .true. simultaneously.
When removebr is true, the boson does not decay.
13.19 jets production, processes 45, 47
These processes represent the production of a boson and jets, including also the effect of a virtual photon when the decays to electrons (nproc=45), but not when it decays to neutrinos. The decays to an pair (nproc=45) or into three species of neutrino (nproc=47). The calculation may be performed at LO only.
When removebr is true, the boson does not decay.
13.20 production, , process 50
These processes represent the production of a boson (or virtual photon) which subsequently decays leptonically, in association with a pair. The effect of the bottom quark mass is included throughout the calculation. The calculation may be performed at LO only, because the one-loop calculation with massive quarks has not yet been performed.
When removebr is true, the boson does not decay.
13.21 production (), processes 51–53
Process 51 is identical to 50 except for the fact that the bottom quark mass is neglected. This allows the calculation to be performed up to NLO. The other processes 52 and 53,also with massless -quarks account for the decays into neutrinos (nproc=52) and bottom quarks (nproc=53). Note that the NLO calculation of process 53 does not currently include radiation from the bottom quarks produced in the decay.
When removebr is true in process 51, the boson does not decay.
13.22 jet production (), process 54
This process represents the production of a boson (and virtual photon) which subsequently decays leptonically, in association with a pair and an additional jet. The effect of the bottom quark mass is neglected throughout and the calculation may be performed at LO only.
When removebr is true, the boson does not decay.
13.23 production (), process 56
Process 56 is the equivalent of 51, with the bottom quarks replaced by charm. Although the charm mass is neglected, the calculation contains diagrams with two gluons in the initial state and a coupling to the heavy quark line – hence the dependence upon the quark flavour.
When removebr is true in process 56, the boson does not decay.
13.24 Di-boson production, processes 61–89
These processes represent the production of a diboson pair , where and may be either a or . All the processes in this section may be calculated at NLO with the exception of nproc=69. There are various possibilities for the subsequent decay of the bosons, as specified in the sections below. Amplitudes for the process at are taken from ref. [70]. We also include singly resonant diagrams at NLO for all processes in the case zerowidth = .false.. For more details on this calculation, please see Refs. [19, 20].
For processes 62, 63, 64, 65, 74 and 75 the default behaviour is that the hadronic decay
products of the bosons are clustered into jets using the supplied jet algorithm parameters, but
no cut is applied on the number of jets. This behaviour can be altered by changing the value
of the variable notag in the file src/User/setnotag.f.
Calculations of processes 61, 71, 76, 81 and 82 can be performed at NLO by subtraction, zero-jettiness slicing and -slicing. They can be computed at NNLO using zero-jettiness slicing and -slicing, as described in ’Non-local slicing approaches for NNLO QCD in MCFM’,[21]. For processes 61, 81 and 86 the NNLO corrections include glue-glue initiated box diagrams which first contribute at order . Two loop results for virtual diagrams at are taken from [7].
13.24.1 production, processes 61-65, 69
For production, both ’s can decay leptonically (nproc=61) or one may decay hadronically (nproc=62 for and nproc=64 for ). Corresponding to processes 62,64, processes 63,65 implement radiation in decay from the hadronically decaying W’s. Process 69 implements the matrix elements for the leptonic decay of both ’s but where no polarization information is retained. It is included for the sake of comparison with other calculations. Processes 62 and 64 may be run at NLO with the option todk, including radiation in the decay of the hadronically decaying . Processes 63 and 65 give the effect of radiation in the decay alone by taking the sum of the choices virt and real, or equivalently tota.
Note that, in processes 62 and 64, the NLO corrections include radiation from the hadronic decays of the .
When removebr is true in processes 61 and 69, the bosons do not decay.
Process 61 can be calculated at NNLO. The NNLO calculations include contributions from the
process
that proceeds through quark loops. The calculation of loops containing
the third quark generation includes the effect of the top quark mass (but
), while the first
two generations are considered massless. For numerical stability, a small cut on the transverse momentum
of the bosons is
applied: GeV
for loops containing massless (first or second generation) quarks,
GeV for
loops. This typically
removes less than %
of the total cross section. The values of these cutoffs can be changed by editing
src/WW/gg_ww.f and recompiling.
13.24.2 production, processes 71–80
This process is calculable at LO,NLO and NNLO and has been treated in several papers, [19, 20, 11, 21]. For production, the is chosen to decay leptonically. The (or virtual photon, when appropriate) may decay into electrons (nproc=71,76), neutrinos (nproc=72,77), a pair of bottom quarks (nproc=73,78), three generations of down-type quarks (nproc=74,79) or two generations of up-type quarks (nproc=75,80). In process 78 the mass of the -quark is neglected. These processes will be observed in the final state as -boson + two or three jets. In processes 72 and 77, a sum is performed over all three species of neutrinos.
When removebr is true in processes 71 and 76, neither the or the boson decays.
13.24.3 with interference, processes 711 and 761
This process can be calculated at LO, NLO, and NNLO. NLO calculations can be performed by subtraction, zero-jettiness slicing and -slicing. NNLO calculations can be performed by zero-jettiness slicing and -slicing.
Full account is taken in this process of the interference between diagrams generated by the exchange of two positrons. This leads to a more complicated resonance structure in the phase space.
13.24.4 production, processes 81–84, 90
The ’s can either both decay leptonically (nproc=81), one can decay leptonically while the other decays into neutrinos (nproc=82) or bottom quarks (nproc=83), or one decays into neutrinos and the other into a bottom quark pair (nproc=84). In process 83 the mass of the -quark is neglected. Note that, in processes 83–84, the NLO corrections do not include radiation from the bottom quarks that are produced by the decay. In process 90 the two bosons decay to identical charged leptons, and interference effects between the decay products of the two bosons are included. In all cases these processes also include the contribution from a virtual photon.
When removebr is true in process 81, neither of the bosons decays.
This process has been treated in several papers, [19, 20, 11, 21]. Processes 81 and 82 can be calculated at NNLO. The NNLO calculation includes contributions from the process that proceeds through quark loops. The calculation of loops containing the third quark generation includes the effect of both the top and the bottom quark mass (), while the first two generations are considered massless. For numerical stability, a small cut on the transverse momentum of the bosons is applied: GeV. This typically removes less than % of the total cross section. The values of these cutoffs can be changed by editing src/ZZ/getggZZamps.f and recompiling.
13.24.5 Anomalous
It is possible to specify anomalous trilinear couplings for the and vertices that are relevant for and production. To run in this mode, one must set zerowidth equal to .true. and modify the appropriate lines for the couplings in input.ini (see below). Note that, at present, the effect of anomalous couplings is not included in the gluon-gluon initiated contributions to the process.
The anomalous couplings appear in the Lagrangian,
as follows (where
represents the usual Standard
Model Lagrangian and
is taken from Ref. [71]): 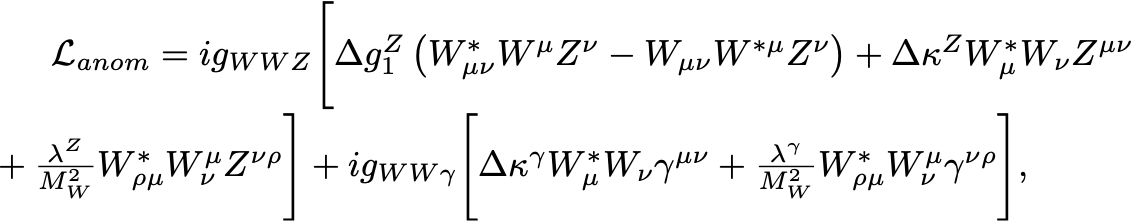
where and the overall coupling factors are , . This is the most general Lagrangian that conserves and separately and electromagnetic gauge invariance requires that there is no equivalent of the term for the photon coupling.
In order to avoid a violation of unitarity, these couplings are often included only after suppression by dipole form factors,
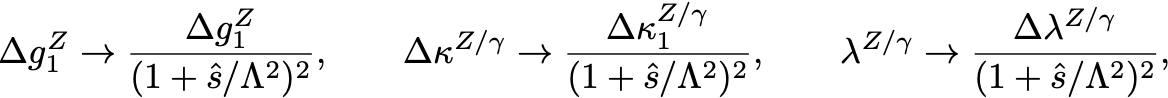
where is the vector boson pair invariant mass and is an additional parameter giving the scale of new physics, which should be in the TeV range. These form factors should be produced by the new physics associated with the anomalous couplings and this choice is somewhat arbitrary. The use of the form factors can be disabled as described below. The file input.ini contains the values of the parameters which specify the anomalous couplings. If the input file contains a negative value for the form-factor scale then the suppression factors described above are not applied.
13.24.6 + interfering, process 8211
This process calculable at leading LO and next-to-leading order NLO. This process describes a specific final state which is accesible both from the decay to two ’s and two ’s. The two processes can thus interfere.
This process has been treated in several papers, [19, 20, 11, 21].
13.25 production, processes 91-100, 900
This process can be calculated at LO, NLO, and NNLO. These processes represent the production of a boson which subsequently decays leptonically, in association with a Standard Model Higgs boson that decays into a tau pair (nproc=91, 96), decays into a -quark pair (nproc=92, 97), a pair of photons (nproc=93, 98), or a pair of -bosons (nproc=94, 99), a pair of bosons (nproc=95, 100). Note that in the cases of Higgs decay to ,() pairs, below the ,() pair threshold one of the ,() bosons is virtual and therefore one must set zerowidth=.false.. The calculation may be performed at NNLO for these processes.
Radiation from the bottom quarks in the decay, an NLO effect, is included in (nproc=920,
970). nproc=900 may be used to compute the sum over both W charges in one run
(with the decay products 3 and 4 representing lepton and antilepton respectively).
This sum is performed by adjustng the CKM matrix to allow both charges of the
boson.
When removebr is .true., neither the boson nor the Higgs decays.
For more information on this process see refs. [22, 11, 21]. NLO calculations can be performed by subtraction, zero-jettiness slicing and -slicing. NNLO calculations can be performed by zero-jettiness slicing and -slicing.
13.26 production, processes 101–110
These processes represent the production of a boson (or virtual photon) in association with a Standard Model Higgs boson that decays into a bottom quark pair (nproc=101-103), or decays into a pair of photons (nproc=104-105) or a pair of bosons (nproc=106-108), or a pair of bosons (nproc=109), or a pair of ’s (nproc=110).
The subsequently decays into either an pair (nproc=101, 106, 109), neutrinos (nproc=102, 107) or a bottom quark pair (nproc=103, 108). The calculation may be performed at NLO, although radiation from the bottom quarks in the decay of the Higgs (or the , for processes 103, 108) is not included. Radiation from the bottom quarks in the decay of the Higgs is included in (nproc=1010).
When removebr is true in processes 101, 106, 109, neither the boson nor the Higgs decays.
For more information on this process see refs. [22, 11, 21]. NLO calculations can be performed by subtraction, zero-jettiness slicing and -slicing. NNLO calculations can be performed by zero-jettiness slicing and -slicing.
13.27 Higgs production, (), processes 111–121
This process is calculable at leading LO, at next-to-leading order NLO, and at next-to-next-to-leading order NNLO.
These processes represent the production of a Standard Model Higgs boson that decays either into a bottom quark pair (nproc=111), a pair of tau’s (nproc=112), a pair that further decays leptonically (nproc=113) a pair where the decays hadronically (nproc=114,115) or a pair (nproc=116-118) . In addition, the loop-level decays of the Higgs into a pair of photons (nproc=119) and the decay are included (nproc=120,121).
For the case of process nproc=115 gives the contribution of radiation from the hadronically decaying . Process 114 may be run at NLO with the option todk, including radiation in the decay of the hadronically decaying . 1 For the case of a decay, the subsequent decays can either be into a pair of muons and a pair of electrons (nproc=116), a pair of muons and neutrinos (nproc=117) or a pair of muons and a pair of bottom quarks (nproc=118).
At LO the relevant diagram is the coupling of two gluons to the Higgs via a top quark loop. This calculation is performed in the limit of infinite top quark mass, so that the top quark loop is replaced by an effective operator. This corresponds to the effective Lagrangian,
| (13.1) |
where is the Higgs vacuum expectation value and the gluon field strength tensor. The calculation may be performed at NLO, although radiation from the bottom quarks in the decay of processes 111 and 118 is not yet included.
When removebr is true in processes 111,112,113,118, the Higgs boson does not decay.
Process 119 implements the decay of the Higgs boson into two photons via loops of top quarks and -bosons. The decay is implemented using the formula Eq.(11.12) from ref. [72]. When removebr is true in process 119 the Higgs boson does not decay.
Processes 120 and 121 implement the decay of the Higgs boson into an lepton-antilepton pair and a photon. As usual the production of a charged lepton-antilepton pair is mediated by a (process 120) and the production of three types of neutrinos by a -boson (process 121). These processes are implemented using a generalization of the formula of [73]. (Generalization to take into account off-shell -boson and adjustment of the sign of in their Eq.(4)).
13.28 production, ( finite), processes 123-127
These processes represent the production of a Higgs boson that decays to , with subsequent decay into leptons. For process 123, the exact form of the triangle loop coupling a Higgs boson to two gluons is included, with both top and bottom quarks circulating in the loop. This is to be contrasted with process 113 in which only the top quark contribution is included in the effective coupling approach.
Process 124 includes only the effect of the interference of the Higgs and
amplitudes, as described in ref. [23]. The calculation is available at LO only. LO corresponds to
in this case. The
calculation of loops containing the third quark generation includes the effect of the top quark mass (but
), while the first
two generations are considered massless. For numerical stability, a small cut on the transverse momentum
of the bosons is
applied: GeV
for loops containing massless (first or second generation) quarks,
GeV for
loops. This typically
removes less than %
of the cross section. The values of these cutoffs can be changed by editing src/HWW/gg_WW_int.f
and recompiling.
Process 125 includes all -initiated diagrams that have a Higgs boson in the -channel, namely the square of the -channel Higgs boson production and the interference with the diagrams that do not contain a Higgs boson, (i.e. ), i.e. .
The result for the square of the box diagrams alone, i.e. the process , may be obtained by running process nproc=61 with part=virt and ggonly=.true.
Process 126 calculates the full result for this process from -initiated diagrams. This includes diagrams that have a Higgs boson in the -channel, the continuum diagrams described above and their interference, i.e. .
Process 127 calculates the full result for this process for -initiated box diagrams alone, , i.e. .
13.29 production, ( finite), processes 128-133
These processes represent the production of a Higgs boson that decays to , with subsequent decay into charged leptons. For process 128, the exact form of the triangle loop coupling a Higgs boson to two gluons is included, with both top and bottom quarks circulating in the loop. This is to be contrasted with process 116 in which only the top quark contribution is included in the effective coupling approach.
Process 129 includes only the effect of the interference of the Higgs and
amplitudes. The calculation is available at LO only. LO corresponds to
in this
case. The calculation of loops containing the third quark generation includes the effect of both
the top quark mass and the bottom quark, while the first two generations are considered
massless. For numerical stability, a small cut on the transverse momentum of the
bosons is applied:
GeV. This typically
removes less than %
of the cross section. The values of these cutoffs can be changed by editing src/ZZ/getggZZamps.f
and recompiling.
Process 130 includes all -initiated diagrams that have a Higgs boson in the -channel, namely the square of the -channel Higgs boson production and the interference with the diagrams that do not contain a Higgs boson, (i.e. ), i.e. .
Process 131 calculates the full result for this process from -intitiated diagrams. This includes diagrams that have a Higgs boson in the -channel, the continuum diagrams described above and their interference, i.e. .
Process 132 gives the result for the square of the box diagrams alone, i.e. the process , i.e. .
Process 133 calculates the interference for the initiated process.
For those processes that include contributions from the Higgs boson, the form of the Higgs propagator may be changed by editing the file src/Need/sethparams.f. If the logical variable CPscheme is changed from the default value .false. to .true. then the Higgs propagator is computed using the “bar-scheme” that is implemented in the HTO code of G. Passarino [74, 75]. The value of the Higgs boson width has been computed with v1.1 of the HTO code, for Higgs masses in the interval GeV. These values are tabulated, in GeV increments, in the file Bin/hto_output.dat. The widths for other masses in this range are obtained by linear interpolation.
13.30 production, processes 1281, 1311, 1321
These processes compute cross sections relevant for the final state , i.e. with charged leptons and neutrinos from the same (electron) doublet. As a result they receive contributions from diagrams with resonant propagators and resonant propagators. Process 1281 only includes amplitudes containing a Higgs boson (c.f. processes 123 and 128). Process 1321 only includes continuum (box-diagram) amplitudes (c.f. processes 127 and 132). Process 1311 includes both amplitudes and the effects of the interference between them (c.f. processes 126 and 131).
13.31 production, processes 1282, 1312, 1322
These processes compute cross sections relevant for the final state , i.e. an electron pair and a sum over all three flavours of neutrino. For muon and tau neutrinos, only diagrams contribute. For electron neutrinos there are contributions from diagrams with resonant propagators and resonant propagators. Process 1282 only includes amplitudes containing a Higgs boson (c.f. processes 123 and 128). Process 1322 only includes continuum (box-diagram) amplitudes (c.f. processes 127 and 132). Process 1312 includes both amplitudes and the effects of the interference between them (c.f. processes 126 and 131).
13.32 production, processes 136–138
These processes represent the production of a Standard Model Higgs boson that decays into a pair of bottom quarks, in association with a further bottom quark. The initial state at lowest order is a bottom quark and a gluon. The calculation may be performed at NLO, although radiation from the bottom quarks in the Higgs decay is not included. For more details on this calculation, please see Ref. [27].
For this process, the matrix elements are divided up into a number of different sub-processes, so the user must sum over these after performing more runs than usual. At lowest order one can proceed as normal, using nproc=136. For a NLO calculation, the sequence of runs is as follows:
- Run nproc=136 with part=virt and part=real (or, both at the same time using part=tota);
- Run nproc=137 with part=real.
The sum of these yields the cross-section with one identified -quark in the final state. To calculate the contribution with two -quarks in the final state, one should use nproc=138 with part=real.
When removebr is .true., the Higgs boson does not decay.
13.33 production with 2 semi-leptonic decays, processes 141–145
These processes describe production including semi-leptonic decays for both the top and the anti-top. Since version 6.2 we have updated this to use the one-loop amplitudes of ref. [29]. The code for the virtual amplitudes now runs about three times faster than earlier versions where the virtual amplitudes of ref. [76] were used. Switching zerowidth from .true. to .false. only affects the bosons from the top quark decay, because our method of including spin correlations requires the top quark to be on shell.
Process 141 includes all corrections, i.e. both radiative corrections to the decay and to the production. This process is therefore the basic process for the description of top production where both quarks decay semi-leptonically. When removebr is true in process 141, the top quarks do not decay. When one wishes to calculate observables related to the decay of the top quark, removebr should be false in process 141. The LO calculation proceeds as normal. At NLO, there are two options:
- part=virt, real or tota : final state radiation is included in the production stage only
- part = todk : radiation is included in the decay of the top quark also and the final result corresponds to the sum of real and virtual diagrams. Note that these runs automatically perform an extra integration, so will take a little longer.
Process 142 includes only the corrections in the semileptonic decay of the top quark. Thus it is of primary interest for theoretical studies rather than for physics applications. Because of the method that we have used to include the radiation in the decay, the inclusion of the corrections in the decay does not change the total cross section. This feature is explained in section 6 of ref. [28].
In the case of process 145, there are no spin correlations in the decay of the top quarks. The calculation is performed by multiplying the spin summed top production cross section, by the decay matrix element for the decay of the and the . These processes may be used as a diagnostic test for the importance of the spin correlation.
13.34 production with decay and a gluon, process 143
This process is only calculable at leading order LO. This process describes lowest order production including two leptonic decays . When removebr is true, the top quarks do not decay. This LO process only includes radiation in production.
13.35 production with one hadronic decay, processes 146–151
This process is calculable at leading LO and next-to-leading order NLO. These processes describe the hadronic production of a pair of top quarks, with one quark decaying hadronically and one quark decaying semi-leptonically. For processes 146–148, the top quark decays semi-leptonically whereas the anti-top quark decays hadronically. For processes 149–151, the top quark decays hadronically whereas the anti-top quark decays semi-leptonically. The base processes for physics are process 146 and 149 which include radiative corrections in both production and decay. Switching zerowidth from .true. to .false. only affects the bosons from the top quark decay, because our method of including spin correlations requires the top quark to be on shell. When one wishes to calculate observables related to the decay of the top quark, removebr should be false in processes 146 and 149. The LO calculation proceeds as normal. At NLO, there are two options:
- part=virt, real or tota : final state radiation is included in the production stage only
- part = todk : radiation is included in the decay of the top quark also and the final result corresponds to the sum of real and virtual diagrams. Note that these runs automatically perform an extra integration, so will take a little longer.
Processes 147 and 150 include only the radiative corrections in the decay of the top quark without including the radiative corrections in the hadronic decay of the -boson. Because of the method that we have used to include the radiation in the decays, the inclusion of the corrections in this stage of the decay does not change the total cross section. Process 148 (151) includes only the radiative corrections in the hadronic decay of the -boson coming from the anti-top (top). The inclusion of the corrections in this stage of the decay increases the partial width by the normal factor.
13.36 production, processes 157–159
These processes are calculable at leading LO and next-to-leading order NLO. These processes calculate the production of heavy quarks (157 for top, 158 for bottom and 159 for charm) up to NLO using the matrix elements of ref. [30]. No decays are included.
13.37 jet production, process 160
This process calculates the production of top quarks and a single jet at LO, without any decay of the top quarks.
13.38 Single-top-quark production and decay at NNLO, process 1610
This calculation is based on ref. [77]. See also ref. [78] for the role of double-DIS scales and the relevancy for PDFs.
This process can be run by using process number 1610. The resulting histograms and cross-sections are printed for a strict fixed-order expansion as well as for a naive addition of all contributions. The fixed-order expansion assembles pieces according to the following formula. Please see ref. [77] for more details.
At each order a corresponding top-decay width is used throughout all parts. The NNLO width is obtained from ref. [79] and at LO and NLO from ref. [80]. These widths agree with numerical results obtained from our calculation of course.
This process can be run with a fixed scale or with dynamic DIS (DDIS) scales by setting
dynamicscale = DDIS, renscale = 1.0 and facscale = 1.0.
At NNLO there are several different contributions from vertex corrections on the
light-quark line, heavy-quark line in production, and heavy-quark line in the top-quark decay.
Additionally there are one-loop times one-loop interference contributions between all three
contributions. These contributions can be separately enabled in the singletop
block:
[singletop]
nnlo_enable_light = .true.
nnlo_enable_heavy_prod = .true.
nnlo_enable_heavy_decay = .true.
nnlo_enable_interf_lxh = .true.
nnlo_enable_interf_lxd = .true.
nnlo_enable_interf_hxd = .true.
nnlo_fully_inclusive = .false.
For a fully inclusive calculation without decay the last setting has to be set to .true. and
the decay and decay interference parts have to be removed. Additionally jet requirements
must be lifted, see below.
When scale variation is enabled with DDIS scales then automatically also a variation around the fixed scale is calculated for comparison.
This process uses a fixed diagonal CKM matrix with
. The setting
removebr=.true. removes the
branching ratio.
This process involves complicated phase-space integrals and we have pre-set the initial
integration calls for precise differential cross-sections with fiducial cuts. The number of calls
can be tuned overall with the multiplier setting integration%globalcallmult. For total
fully inclusive cross-sections the number of calls can be reduced by a factor of ten by setting
integration%globalcallmult = 0.1, for example.
For scale variation uncertainties and PDF uncertainties we recommend to
start with the default number of calls and a larger number of warmup iterations
integration%iterbatchwarmup=10, for example. For the warmup grid no scale
variation or PDF uncertainties are calculated and this ensures a good Vegas integration
grid that can be calculated fast. The setting integration%callboost modifies the
number of calls for subsequent integration iterations after the warmup. For example
setting it to 0.1 reduces the calls by a factor of ten. This is typically enough to
compute the correlated uncertainties for a previously precisely determined central
value.
At NNLO the default value for is , which is the value used for all the plots in our publication. We find that cutoff effects are negligible at the sub-permille level for this choice. We strongly recommend to not change this value.
Using the plotting routine with b-quark tagging
The calculation has been set up with b-quark tagging capabilities that can be accessed in
both the gencuts_user.f90 routine and the plotting routine nplotter_singletop_new.f90.
The plotting routine is prepared to generate all histograms shown in our publication in
ref. [77]. By default the top-quark is reconstructed using the leading b-quark jet and
the exact W-boson momentum, but any reconstruction algorithm can easily be
implemented.
The version of the gencuts_user.f90 file used for the plots in our paper [77] is available
as gencuts_user_singletop_nnlo.f90. It can be used as a guide on how to access the
b-quark tagging in the gencuts_user routine.
See also nplotter_ktopanom.f (used for the NLO off-shell calculation in ref. [33] for a reconstruction
of the W-boson. It is based on requiring an on-shell W-boson and selecting the solution for the neutrino
-component
that gives the closest on-shell top-quark mass by adding the leading b-quark jet.
Calculating fully inclusive cross-sections
When calculating a fully inclusive cross-section without top-quark decay please set
zerowidth = .true., removebr = .true. in the general section of the input file; inclusive
= .true, ptjetmin = 0.0, etajetmax = 99.0 in the basicjets section; makecuts =
.false. in the cuts section; also set nnlo_enable_heavy_decay = .false. and
nnlo_enable_interf_lxd = .false., nnlo_enable_interf_hxd = .false. and
nnlo_fully_inclusive = .true. in the singletop section.
These settings ensure that neither the decay nor any production times decay interference contributions are included. The last setting makes sure that only the right pieces in the fixed-order expansion of the cross-section are included. It also ensures that the b-quark from the top-quark decay is not jet-tagged and just integrated over.
Notes on runtimes and demo files
Running the provided input file input_singletop_nnlo_Tevatron_total.ini with -integration%globalcallmult=0.1 and
without histograms takes about 4-5 CPU days. So depending on the number of cores, this can
be run on a single desktop within a few hours.
Running the input file input_singletop_nnlo_LHC_fiducial.ini with the default set of calls and histograms takes
about 3 CPU months (about 3 wall-time hours on our cluster with 45 nodes). For the fiducial
cross-section (without precise histograms) a setting of -integration%globallcallmult=0.2
can also be used.
Note that -extra%nohistograms = .true. has been set in these demonstration files, so
no further histograms from nplotter_singletop_new.f90 are generated.
The input file input_singletop_nnlo_LHC_fiducial.ini together with the file
gencuts_user_singletop_nnlo.f90. replacing src/User/gencuts_user.f90 reproduces the
fiducial cross-sections in ref. [77] table 6.
13.39 Single-top-quark production and decay at NNLO, process 1650
This calculation is based on ref. [77]. This process constitutes the real correction needed for the complete NNLO order calculation. In other words it is the plus-one-jet process evaluated at NLO.
13.40 Off-shell single top production in SM and SMEFT, processes 164,169
The processes 164 and 169 represent off-shell single-top-quark and anti-top-quark production, respectively. The calculations are performed in the complex-mass scheme. Both the SM and contributions from the SMEFT can be calculated. For more details on this calculation, please refer to ref. [33].
Dynamical double deep inelastic scattering scales can be
consistently used at NLO by setting dynamicscale to ‘DDIS’ and
scalefacscale
to 1d0. In this way the momentum transfer along the
-boson
is used as the scale for the
light-quark-line corrections ,
and
for the heavy-quark-line corrections. These scales are also consistently
used for the non-resonant contributions, with QCD corrections on the
-quark
line, and separate QCD corrections on the bottom-quark line.
The new block ‘Single top SMEFT, nproc=164,169’ in the input file governs the
inclusion of SMEFT operators and corresponding orders. The scale of new physics
can be separately set, and has a default value of
GeV. The flag enable
1/lambda4 enables the
contributions, where operators
and
can contribute for the first time. For the non-Hermitian operators we allow complex Wilson
coefficients. We also have a flag to disable the pure SM contribution, leaving only contributions
from SMEFT operators either interfered with the SM amplitudes or as squared contributions
at .
This can be used to directly and quickly extract kinematical distributions and the magnitudes
of pure SMEFT contributions.
To allow for easier comparisons with previous anomalous couplings results, and possibly estimate further higher order effects, we allow for an anomalous couplings mode at LO by enabling the corresponding flag. The relations between our operators and the anomalous couplings are
where is the -boson mass, and has been used to derive this equivalence. Note that the minus sign for and is different from the literature. See also the publication [33] for more information.
For comparisons with on-shell results one needs to add up the contributions from processes 161 at NLO and from the virt and real contributions from 162, see above.
The analysis/plotting routine is contained in the file ‘src/User/nplotter_ktopanom.f’,
where all observables presented in this study are implemented, and the
-boson/neutrino
reconstruction is implemented and can be switched on or off.
13.41 production, processes 180–187
These processes represent the production of a boson that decays leptonically in association with a top quark. The lowest order diagram involves a gluon and a bottom quark from the PDF, with the -quark radiating a boson and becoming a top quark. The calculation can be performed up to NLO. For more details on this calculation, please see Ref. [34].
Processes 180 and 185 produce a top quark that does not decay, whilst in processes 181 and 186 the top quark decays leptonically. Consistency with the simpler processes (180,185) can be demonstrated by running process 181,186 with removebr set to true.
At next-to-leading order, the calculation includes contributions from diagrams with two gluons in the initial state, . The of the additional quark is vetoed according to the value of the parameter ptmin_bjet which is specified in the input file. The contribution from these diagrams when the of the quark is above ptmin_bjet is zero. The values of this parameter and the factorization scale (facscale) set in the input file should be chosen carefully. Appropriate values for both (in the range - GeV) are discussed in the associated paper [34].
When one wishes to calculate observables related to the decay of the top quark, removebr should be false. The LO calculation proceeds as normal. At NLO, there are two options:
- part=virt, real or tota : final state radiation is included in the production stage only
- part = todk : radiation is included in the decay of the top quark also and the final result corresponds to the sum of real and virtual diagrams. This process can only be performed at NLO with zerowidth = .true. This should be set automatically. Note that these runs automatically perform an extra integration, so will take a little longer.
The contribution from radiation in the decay may be calculated separately using processes 182,187. These process numbers can be used with part=virt,real only. To ensure consistency, it is far simpler to use 181,186 and this is the recommended approach.
13.42 Di-jet production, processes 190–191
Process 190 represents di-jet production through strong interactions. It may be calculated to LO only.
Process 191 is an ancillary process that is used in the calculation of weak one-loop corrections to di-jet production. This process is calculable at leading LO and next-to-leading order NLO. When computed at LO it gives the contribution of weak () and mixed weak-strong () mediated processes to di-jet production. Please refer to Ref. [35] for details.
13.43 jet production, finite, process 200
This process represents the production of a Higgs boson in association with a single jet based on refs. [81, 82, 83, 84, 40, 41]. Decay modes are currently unsupported/untested. The top-quark mass is taken into account exactly for the Born and real-emission parts, as well as for the singular part of the virtual corrections. The real emission calculation is based on the one-loop, Higgs boson + 4 parton calculations with full quark masss effects of ref.[40, 41].
The finite part of the two-loop virtual corrections can be computed in different ways by setting the input file parameter mtex.
- In a low energy asymptotic expansion in up to order by setting mtex to or in the input file. This is recommended for transverse momenta up to GeV.
- In a high energy expansion by setting mtex=100 in the input file. This is recommended for transverse momenta beyond GeV.
- In a rescaling approach where the finite part of the two-loop virtual amplitude in the effective field theory () is rescaled pointwise by the ratio of the one-loop amplitude computed with full dependence to the one-loop amplitude for . This mode is the default mode and enabled with mtex=0 in the input file. This is the recommended approach for the intermediate energy region and for estimating top-mass uncertainties in the transition regions between these approaches.
This process is therefore calculable at leading LO and at next-to-leading order NLO (using an approximation for the two loop matrix element). Full NLO calculations (with the exact two-loop matrix element) have been performed in refs. [85, 86, 87].
13.44 jet production, processes 201–210
These processes represent the production of a Higgs boson in association with a single jet, with the subsequent decay of the Higgs to either a pair of bottom quarks (processes 201,203,206) or to a pair of tau’s (202,204,207), or to a pair of ’s which decay leptonically (208), or to a pair of ’s which decay leptonically (209), or to a pair of photons (210).
13.44.1 finite, 201,202,206,207
The Higgs boson couples to a pair of gluons via a loop of heavy fermions which, in the Standard Model, is accounted for almost entirely by including the effect of the top quark alone. For processes 201,202,206,207, the matrix elements include the full dependence on the top quark mass. The calculation can only be performed at LO. The LO full dependence calculation implements results of refs.[83, 84]. However, the Higgs boson can either be the Standard Model one (processes 201,202) or a pseudoscalar (206,207). Note that the pseudoscalar case corresponds, in the heavy top limit, to the effective Lagrangian,
| (13.2) |
where . The interaction differs from the scalar case in by a factor of and hence the rate is increased by a factor of .
13.44.2 , 203,204,208,209,210
For processes 203,204,208,209,210, the calculation is performed in the limit of infinite top quark mass, so that NLO and NNLO results can be obtained. The virtual one-loop matrix elements have been implemented from refs [88] and [89]. Phenomenological results have previously been given in refs. [90],[88] and [91]. Note that the effect of radiation from the bottom quarks in process 203 is not included. NNLO corrections have only been implemented for processes 204 and 210, using the 1-jettiness slicing approach described in ref. [92]. When removebr is true in processes 201, 203, 206, 208, 209 and 210, the Higgs boson does not decay.
13.45 Higgs production via WBF, processes 211–217
These processes provide predictions for the production of a Higgs boson in association with two jets via weak-boson fusion (WBF). The Higgs boson subsequently decays to either a pair of bottom quarks (processes 211, 216), to a pair of tau’s (212, 217), to a pair of bosons (213), to a pair of bosons (214), or to a pair of photons (215). For more details on this calculation, please see Ref. [36].
Calculations can be performed up to NLO for processes 211–215. In addition to this, processes 216 and 217 provide the lowest order calculation of the WBF reaction which radiates an additional jet.
When removebr is true, the Higgs boson does not decay.
13.46 -pair production via WBF, processes 220,2201,222,2221
The weak processes (nproc=220,222) occur in , whereas the strong processes (nproc=2201,2221) occur in . These processes can currently only be calculated at lowest order.
13.47 production, process 221
This process provides predictions for the production of a tau lepton pair mediated by , with subsequent leptonic decays. The calculation is available at LO only. The relevant matrix elements are adapted from the ones in ref. [93].
When removebr is true, the tau leptons do not decay.
13.48 -pair production via WBF, processes 223,2231
The weak process (nproc=223) occurs in , whereas the strong process occurs (nproc=2231) in . These processes can currently only be calculated at lowest order.
13.49 -pair production via WBF, processes 224,2241
The weak process (nproc=224) occurs in , whereas the strong process (nproc=2241) occurs in . These processes can currently only be calculated at lowest order.
13.50 -pair production via WBF, processes 225,2251
The weak process occurs in , whereas the strong process occurs in . These processes can currently only be calculated at lowest order.
13.51 -pair production via WBF, processes 226
This weak process occurs at , and contains contributions, from both and production. This process can currently only be calculated at lowest order.
13.52 -pair production via WBF, processes 228,2281
The weak process (nproc=228) occurs in , whereas the strong process occurs (nproc=2281) in . These processes can currently only be calculated at lowest order.
13.53 -pair production via WBF, processes 229,2291
The weak process (nproc=229) occurs in , whereas the strong process occurs (nproc=2291) in . These processes can currently only be calculated at lowest order.
13.54 -channel single top with an explicit -quark, processes 231–240
These represent calculations of the -channel single top (231) and anti-top (231) processes in a scheme with four flavours of quark in the proton, so that -quarks are not present in the proton. The -quark is instead explicitly included in the final state. For more details on this calculation, please see Ref. [32].
Processes 232 and 236 represent -channel single top production in association with a further jet and may be calculated at LO only.
Processes 233 and 238 are the complete four-flavour scheme -channel single top production processes. These are therefore the processes that should be used for most physics applications. When one wishes to calculate observables related to the decay of the top quark, removebr should be false in processes 233 and 236. The LO calculation proceeds as normal. At NLO, there are two options:
- part=virt, real or tota : final state radiation is included in the production stage only
- part = todk : radiation is included in the decay of the top quark also and the final result corresponds to the sum of real and virtual diagrams. Note that these runs automatically perform an extra integration, so will take a little longer.
Processes 234 and 239 give the extra contribution due to radiation in top decay. These processes are mainly of theoretical interest.
Processes 235 and 240 are the leading order single top processes with an extra radiated parton. These processes do not includes jets produced in the decay process.
13.55 jets production, processes 251,252
These processes represent the production of two bosons in association with two (process 251) or three (process 252) jets. The lowest order at which two positively charged bosons can be produced is with two jets. This process is only implemented for leptonic decays of the particles. The calculation is available at LO only. The calculation and code are from ref. [39]. removebr is not implemented and has no effect.
13.56 + 2 jet production, process 253-254
These processes represent the production of and bosons in association with two jets. This process is only implemented for leptonic decays of the and particles. The calculation is available at LO only.
13.57 + + jet production, process 255-256
These processes represent the production of and bosons in association with two jets, one of which contains a -quark. This process is only implemented for leptonic decays of the and particles. The calculation is available at LO only.
13.58 + 2 production, process 259-260
These processes represent the production of and bosons in association with two -quark jets. This process is only implemented for leptonic decays of the and particles. The calculation is available at LO only.
13.59 production, processes 261–267
These processes represent the production of a boson that decays into a pair of electrons, in association with a heavy quark, . For more details on this calculation, please see Ref. [94].
For processes 261, 262, 266 and 267 the initial state at lowest order is the heavy quark and a gluon and the calculation may be performed at NLO. As for production, the matrix elements are divided into two sub-processes at NLO. Thus the user must sum over these after performing more runs than usual. At lowest order one can proceed as normal, using nproc=261 (for ) or nproc=262 (for ). For a NLO calculation, the sequence of runs is as follows:
- Run nproc=261 (or 262) with part=virt and part=real (or, both at the same time using part=tota);
- Run nproc=266 (or 267) with part=real.
The sum of these yields the cross-section with one identified heavy quark in the final state when inclusive is set to .false. . To calculate the rate for at least one heavy quark, inclusive should be .true..
For processes 263 and 264, the calculation uses the matrix elements for the production of a and a heavy quark pair and demands that one of the heavy quarks is not observed. It may either lie outside the range of and required for a jet, or both quarks may be contained in the same jet. Due to the extra complexity (the calculation must retain the full dependence on the heavy quark mass), this can only be computed at LO.
When removebr is true, the boson does not decay.
13.60 Higgs+2 jet,processes 269
13.61 jet production, , processes 270–274
These processes represent the production of a Standard Model Higgs boson in association with two jets. The Higgs boson subsequently decays to either a pair of photons (nproc=270), a bottom quark pair (nproc=271), a pair of tau’s (nproc=272), a pair of leptonically decaying ’s (nproc=273) or a pair of leptonically decaying ’s (nproc=274).
The matrix elements are included in the infinite top mass limit using the effective Lagrangian approach.
When removebr is true, the Higgs boson does not decay.
13.62 jet production, (), processes 275-279
These processes represent the production of a Standard Model Higgs boson in association with three jets. The Higgs boson subsequently decays to either a bottom quark pair (nproc=275), or a pair of tau’s (nproc=276) or a pair of ’s that decay leptonically into a single generation of leptons (nproc=278) or a pair of ’s that decay leptonically into a single generation of leptons (nproc=279). The matrix elements are included in the infinite top mass limit using an effective Lagrangian approach. These calculations can be performed at LO only.
When removebr is true, the Higgs boson does not decay.
13.63 Direct production, processes 280–282
These processes represent the production a real photon. Since this process includes a real photon, the cross section diverges when the photon is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. This will ensure that the cross section is well-defined.
Currently the code computes this process up to NLO accuracy. The extension to NNLO [95, 96, 97] has not yet been made public.
13.64 Direct + heavy flavour production, processes 283–284
These processes represent the production a real photon with a quark or a quark Since this process includes a real photon, the cross section diverges when the photon is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. This will ensure that the cross section is well-defined.
The calculation of process 283–284 is only available at leading order.
13.65
This process computes the contribution of light-quark loops to the process . It is calculable at leading LO and next-to-leading order NLO. The calculation and a phenomenological analysis are described in Ref. [43]. This process includes the one-loop gluon-gluon contribution as given in ref. [98].
13.66 , (top loops at LO)
This process calculable at leading LO and next-to-leading order NLO.
This process computes the contribution of quark loops ( light quarks and top quarks) to the process . It is calculable at leading LO and next-to-leading order NLO, although the effect of top-quark loops are only included at LO. The calculation and a phenomenological analysis are described in Ref. [43].
13.67 Diphoton production
Process 285 represents the production of a pair of real photons. Since this process includes two real photons, the cross section diverges when one of the photons is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both ptmin and etamax. This will ensure that the cross section is well-defined.
The calculation of process 285 may be performed using either the Frixione algorithm or standard cone isolation. Since version 10.1 also a fixed cone size can be specificed as well as a simple hybrid cone isolation, see ref. [99].
This process also includes the one-loop gluon-gluon contribution as given in ref. [98]. The production of a photon via parton fragmentation is included at NLO and can be run separately by using the frag option in part. This option includes the contributions from the integrated photon dipole subtraction terms and the LO QCD matrix element multiplied by the fragmentation function.
The phase space cuts for the final state photons are defined in input.ini, for multiple photon processes such as 285 - 287 the ’s of the individual photons (hardest, second hardest and third hardest or softer) can be controlled independently.The remaining cuts on , etc. are applied universally to all photons. Users wishing to alter this feature should edit the file photon_cuts.f in the directory src/User.
This process can be calculated at LO, NLO, and NNLO. NLO calculations can be performed by subtraction, zero-jettiness slicing and -slicing. NNLO calculations can be performed by zero-jettiness slicing and -slicing. Input files for these 6 possibilities are given in the link below.
The fixed-order NNLO calculation has been implemented in ref. [43]. Transverse momentum resummation at the level of has been implemented in ref. [100]. By including the three-loop hard [101] and beam functions [102],[103],[104] it has been upgraded to in ref. [99].
13.67.1 Transverse momentum resummation
Transverse momentum resummation can be enabled for process 285 at highest order with ‘part=resNNLOp‘. The setting ‘part=resNNLO‘ resums to order ( accuracy in improved perturbation theory power counting) and ‘part=resNLO‘ to order . Note that process 285 with resummation only includes the channel. The channel enters at an increased relative level of , so has to be added with process number 2851 at order ‘part=resNLO‘ for overall precision. For an overall consistent precision of the channel can be added with ‘part=resLO‘.
Note that at fixed-order the channel is included at NNLO automatically at the level of .
The fixed-order NNLO calculation has been implemented in ref. [43]. Transverse momentum resummation at the level of NLL+NNLO has been implemented in ref. [100]. By including the three-loop hard [101] and beam functions [102],[103],[104] it has been upgraded to NLL’ in ref. [99].
13.68
Process 2861 represents the process mediated by a loop of light quarks. This process is calculable at leading order LO, O().
The calculation is described in Ref. [105].
13.69 jet production, process 286
Process 286, corresponding to the production of a pair of real photons in association with a jet, can be computed at NLO. Since this process includes two real photons, the cross section diverges when one of the photons is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. This will ensure that the cross section is well-defined.
The calculation of process 286 may be performed at NLO using either the Frixione algorithm [55] or standard cone isolation. This process also includes the one-loop gluon-gluon contribution as given in ref. [98]. The production of a photon via parton fragmentation is included at NLO and can be run separately by using the frag option in part. This option includes the contributions from the integrated photon dipole subtraction terms and the LO QCD matrix element multiplied by the fragmentation function.
The phase space cuts for the final state photons are defined in input.ini, for multiple photon processes such as 285 - 287 the ’s of the individual photons (hardest, second hardest and third hardest or softer) can be controlled independently. The remaining cuts on , etc. are applied universally to all photons. Users wishing to alter this feature should edit the file photon_cuts.f in the directory src/User.
The calculation is described in Ref. [105].
13.70 production, process 287
Process 287 represents the production of three real photons. The cross section diverges when one of the photons is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. This will ensure that the cross section is well-defined.
The calculation of process 285 may be performed at NLO using either the Frixione algorithm [55] or standard cone isolation. The production of a photon via parton fragmentation is included at NLO and can be run separately by using the frag option in part. This option includes the contributions from the integrated photon dipole subtraction terms and the LO QCD matrix element multiplied by the fragmentation function. The phase space cuts for the final state photons are defined in input.ini, for multiple photon processes such as 285 - 287 the ’s of the individual photons (hardest, next-to hardest and softest) can be controlled independently. The remaining cut on , etc. are applied universally to all photons. Users wishing to alter this feature should edit the file photon_cuts.f in the directory src/User.
13.71 production, process 289
Process 289 represents the production of four real photons. The cross section diverges when one of the photons is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. This will ensure that the cross section is well-defined.
The calculation of process 289 may be performed at NLO using either the Frixione algorithm [55] or standard cone isolation. The production of a photon via parton fragmentation is included at NLO and can be run separately by using the frag option in part. This option includes the contributions from the integrated photon dipole subtraction terms and the LO QCD matrix element multiplied by the fragmentation function. The phase space cuts for the final state photons are defined in input.ini, for multiple photon processes such as 285 - 289 the ’s of the individual photons (hardest, next-to hardest and softest) can be controlled independently. The remaining cut on , etc. are applied universally to all photons. Users wishing to alter this feature should edit the file photon_cuts.f in the directory src/User.
Note that for this process the second softest and softest photons are forced to have equal minimum , defined by the [gammptmin(3rd)] variable in the input file.
13.72 production, processes 290-299, 2941, 2991
These processes represent the production of a boson which subsequently decays leptonically, in association with a real photon. Since this process includes a real photon, the cross section diverges when the photon is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. Moreover, when the parameters zerowidth and removebr are set to .false. the decay will include photon radiation from the lepton, so that a non-zero (Rgalmin) should also be supplied. This will ensure that the cross section is well-defined. Virtual amplitudes are taken from ref. [70].
The calculation of processes 290 and 295 may be performed at NLO and NNLO using the Frixione algorithm [55] or standard isolation. The phenomenology of these processes at NNLO has been treated in ref. [12]. The one-loop virtual diagrams are taken from [70] and the two-loop virtual diagrams are taken from [106]. For processes 290 and 295 the role of mtrans34cut changes to become a cut on the transverse mass on the system, i.e. the photon is included with the leptons in the cut.
Processes 292 and 297 represent the +jet production processes. They may be computed to NLO.
Processes 294 and 299 represent the photon-induced reactions, and should be computed at NLO. Processes 2941 and 2991 represent the photon-induced reactions, and should be computed at NLO.
13.72.1 Anomalous couplings
Processes 290-297 may also be computed including the effect of anomalous couplings, making use of the amplitudes calculated in Ref. [107]. Including only dimension 6 operators or less and demanding gauge, and invariance gives the general form of the anomalous vertex [107],
where the overall coupling has been chosen to be . The parameters that specify the anomalous couplings, and , are specified in the input file as already discussed in Section 13.24. If the input file contains a negative value for the form-factor scale then no suppression factors are applied to the anomalous couplings. Otherwise, the couplings are included in MCFM only after suppression by dipole form factors,
| (13.4) |
where is the pair invariant mass.
The Standard Model cross section is obtained by setting .
13.73 , production, processes 300, 305
Processes 300 and 305 represent the production of a boson (or virtual photon for process 300) in association with a real photon based on ref. [108]. The subsequently decays into either an pair (nproc=300) or neutrinos (nproc=305). Since these processes include a real photon, the cross section diverges when the photon is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. Moreover, when the parameters zerowidth and removebr are set to .false. the decay (nproc=300) will include photon radiation from both leptons, so that a non-zero (Rgalmin) should also be supplied. This will ensure that the cross section is well-defined. The calculation of processes 300 may be performed at NNLO using the Frixione algorithm [55] or standard isolation. The one-loop virtual diagrams are taken from [70] and the two-loop virtual diagrams are taken from [106].
For the process 300 the role of mtrans34cut changes to become a cut on the invariant mass on the system, i.e. the photon is included with the leptons in the cut.
13.73.1 Anomalous and couplings
Processes 300-305 may also be computed including the effect of anomalous couplings between bosons and photons. Note that, at present, the effect of anomalous couplings is not included in the gluon-gluon initiated contributions.
The anomalous vertex (not present at all in the Standard Model), considering operators up to dimension 8, is given by [107],
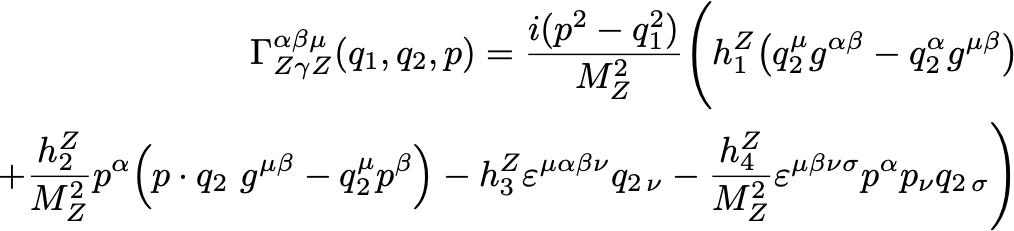
where the overall coupling has been chosen to be (and ). The non-standard momentum-space vertex can be obtained from this equation by setting and replacing . The parameters that specify the anomalous couplings, and (for ), are specified in the input file as, e.g. h1(Z) and h1(gamma). If the input file contains a negative value for the form-factor scale then no suppression factors are applied to these anomalous couplings. Otherwise, the couplings are included in MCFM only after suppression by dipole form factors,
| (13.5) |
where is the pair invariant mass. Note that these form factors are slightly different from those discussed in Sections 13.24 and 13.72. The form factors can be modified in src/Need/set_anomcoup.f.
The Standard Model cross section is obtained by setting for .
13.74 production processes, 301, 306
Processes 301 and 306 represent the production of a boson (or virtual photon for process 301) in association with two photons. The subsequently decays into either an pair (nproc=301) or neutrinos (nproc=306). Since these processes include real photons, the cross section diverges when either of the photons is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. Moreover, when the parameters zerowidth and removebr are set to .false. the decay (nproc=301) will include photon radiation from both leptons, so that a non-zero (Rgalmin) should also be supplied. This will ensure that the cross section is well-defined. Anomalous couplings are not currently implemented for these processes.
13.75 , production, processes 302, 307
Processes 302 and 307 represent the production of a boson (or virtual photon) in association with a real photon and at least one jet. The subsequently decays into either an pair (nproc=302) or neutrinos (nproc=307). Since these processes include a real photon and a jet, the cross section diverges when the photon or jet is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax, and ptjetmin and etajetmax. Moreover, when the parameters zerowidth and removebr are set to .false., the decay (nproc=302) will include photon radiation from both leptons, so that a non-zero (Rgalmin) should also be supplied. This will ensure that the cross section is well-defined. The calculation of processes 302 and 307 may be performed at NLO using the Frixione algorithm [55] or standard isolation. Anomalous couplings are not currently implemented for these processes.
13.76 and , 303, 304, 308 and 309
These processes are available at LO only. The subsequently decays into either an pair (nproc=303,304) or neutrinos (nproc=308,309). Since these processes include a real photon and a jet, the cross section diverges when a photon or a jet is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax, and ptjetmin and etajetmax. Moreover, when the parameters zerowidth and removebr are set to .false. the decay (nproc=303, 304) will include photon radiation from both leptons, so that a non-zero (Rgalmin) should also be supplied. This will ensure that the cross section is well-defined. Anomalous couplings are not currently implemented for these processes.
13.77 jet production processes 311–326
These processes represent the production of a boson that decays leptonically, in association with a heavy quark, and an additional light jet. In processes 311 and 316, is a bottom quark, whilst processes 321 and 326 involve a charm quark. In these processes the quark occurs as parton PDF in the initial state. The initial state in these processes consists of a light quark and a heavy quark, with the light quark radiating the boson. These calculations may be performed at LO only.
When removebr is true, the boson does not decay.
13.78 jet production, processes 331, 336
These processes represent the production of a boson that decays leptonically, in association with a charm quark and an additional light jet.
In contrast to processes 321 and 326 described above, the initial state in this case consists of two light quarks, one of which is a strange quark which radiates the boson. The calculation may be performed at LO only.
When removebr is true, the boson does not decay.
13.79 jet production, processes 341–357
These processes represent the production of a boson that decays into a pair of electrons, in association with a heavy quark, and an untagged jet. For more details on this calculation, please see Ref. [109].
For processes 341 and 351 the initial state at lowest order is the heavy quark and a gluon and the calculation may be performed at NLO. Thus in these processes the quark occurs as parton PDF in the initial state. As for and production, the matrix elements are divided into two sub-processes at NLO. Thus the user must sum over these after performing more runs than usual. At lowest order one can proceed as normal, using nproc=341 (for ) or nproc=351 (for ). For a NLO calculation, the sequence of runs is as follows:
- Run nproc=341 (or 351) with part=virt and part=real (or, both at the same time using part=tota);
- Run nproc=342 (or 352) with part=real.
The sum of these yields the cross-section with one identified heavy quark and one untagged jet in the final state when inclusive is set to .false. . To calculate the rate for at least one heavy quark and one jet (the remaining jet may be a heavy quark, or untagged), inclusive should be .true..
Processes 346,347 and 356,357 are the lowest order processes that enter the above calculation in the real contribution. They can be computed only at LO.
When removebr is true, the boson does not decay.
13.80 , processes 361–363
These processes represent the production of a from a charm and anti-strange quark at LO. The boson decays into a neutrino and a positron.
The NLO corrections to this LO process include a contribution of the form, . For process 361 this contribution is calculated in the approximation at NLO. In order to perform the NLO calculation for a non-zero value of , one must instead sum the results of processes 362 and 363 for part=tota.
13.81 production, processes 370-371
These processes represent the production of a boson which subsequently decays leptonically, in association with two real photons. Since this process includes real photons, the cross section diverges when the photon is very soft or in the direction of the beam. Thus in order to produce sensible results, the input file must supply values for both gammptmin and gammrapmax. Moreover, when the parameters zerowidth and removebr are set to .false. the decay will include photon radiation from the lepton, so that a non-zero R(photon,lept)_min should also be supplied. This will ensure that the cross section is well-defined.
These processes may be computed at leading order only.
13.82 production in the 4FNS, processes 401–408
These processes represent the production of a boson and one or more jets, at least one of which is a -quark, calculated in the 4-flavour number scheme (4FNS). This implies that contributions that explicitly contain a -quark in the initial state are not included. These processes all use the same matrix elements as processes 20 and 25 (see section 13.8), but make different cuts on the final state. The final state is specified by the process number and the value of the flag inclusive, as shown in Table 13.1. An additional flag is hard-coded into the file src/Cuts/filterWbbmas.f to control the inclusion of the 3-jet configuration, when inclusive is set to .true.. By default, the statement veto3jets = .false. is included in this file. If this flag is set to .true. then the contribution is not included in processes 401, 402, 406, 407.
| Process (/) | inclusive=.false. | inclusive=.true. |
| 401/406 | or | + () or () or () |
| 402/407 | + () | |
| 403/408 | (no extra configurations) | |
As usual, jets may be unobserved as a result of them falling outside the and rapidity ranges specified in the input file. In addition, the number of jets may be different from the number of partons in the matrix element calculation as a result of merging in the jet algorithm.
13.83 production in the 5FNS, processes 411, 416
These processes represent production of a boson in association with a -jet, computed in the 5-flavour number scheme, i.e. a -quark is present in the initial state. The lowest order processes are the same as in processes 311, 316. The results at NLO are not physical cross sections since part of the corrections are not included in order to avoid double-counting with the 4FNS process (processes 401 and 406). To obtain combined 4FNS+5FNS predictions, the user should select process 421 () or 426 ().
13.84 production in combined 4FNS/5FNS, processes 421, 426
These processes represent the production of a boson and one or more jets, at least one of which is a -quark, calculated by combining the 4- and 5-flavour results of processes 401, 411 (for 421) and 406, 416 (for 426). The selection of the final state is the same as for processes 401 and 406, as described in Section 13.82. The procedure for combining the two calculations is described in refs. [110, 111].
13.85 jet production, processes 431,436
These processes represent the production of a boson which subsequently decays leptonically, in association with a pair and an additional jet. The effect of the bottom quark mass is included (in contrast to the massless approximation used in processes 24, 29) and the calculation may be performed at LO only.
When removebr is true, the boson does not decay.
13.86 Diboson+jet production, processes 461–487
These processes represent the production of a vector boson pair in association with a jet.
They are the counterparts of the corresponding diboson process (nproc-400) described above,
but also including a jet in the final state. They may be computed to NLO. Amplitudes are
taken from refs. [44, 45, 46].
13.87 processes 500–516
These processes represent the production of a boson which subsequently decays leptonically, in association with a pair. In all except processes 500 and 510 the decays of the top and anti-top quark are included. Processes 501,502 and 511,512 refer to the semileptonic decay of the top and antitop quarks, with the latter process in each pair giving the radiation in the decay of the top and antitop. Process 503 (513) refers to the semileptonic decay of the top (antitop) and the hadronic decay of the antitop (top). Processes 506(516) gives the semileptonic decay of the antitop(top) and the hadronic decay of the top(antitop). Processes 506(516) do not give same sign lepton events, so they may be of less phenomenological importance. For this reason we have not yet included radiation in the decay for these processes.
For processes 503, 506, 513 and 516 the default behaviour is that the hadronic decay products are clustered into jets using the supplied jet algorithm parameters, but no cut is applied on the number of jets. This behaviour can be altered by changing the value of the variable notag in the file src/User/setnotag.f.
The top quarks are always produced on-shell, which is a necessity for a gauge invariant result from this limited set of diagrams, but all spin correlations are included. Switching zerowidth from .true. to .false. only affects the bosons (both the directly produced one and from the top quark decay). Processes 501 and 511 may be run at NLO with the option todk, including radiation in the decay of the top quark, see section 13.33.
13.88 production, processes 529-533
These processes represent the production of a boson in association with a pair of top quarks. These processes are only available at LO. For process 529, neither the top quarks nor the -boson decays. In processes 530-533, the top quarks are always produced on-shell, which is a necessity for a gauge invariant result from this limited set of diagrams. Switching zerowidth from .true. to .false. only affects the and the bosons from the top quark decay. In process 530 the boson decays into an electron pair, whilst in 531 the decay is into a massless bottom quark pair. In process 532–533 the boson decays into an electron pair, whilst one or other of the top quark or top anti-quark decays hadronically.
For processes 532 and 533 the default behaviour is that the hadronic decay products are clustered into jets using the supplied jet algorithm parameters, but no cut is applied on the number of jets. This behaviour can be altered by changing the value of the variable notag in the file src/User/setnotag.f.
When removebr is true in process 530, the top quarks and the boson do not decay.
13.89 and production, processes 540–557
These processes describe the production of a single top quark (540, 544, 550, 554) or antiquark (541, 547, 551, 557) by exchange in the -channel, in association with a Higgs boson. These processes can be performed at NLO. For processes 540, 541, 550, 551, the top quark does not decay, but the Higgs boson decays to , (540, 541), or to , (550, 551). Processes 544, 547 and 554, 557 include the decay of the top quark and antiquark in the approximation in which the top quark is taken to be on shell allowing a clean separation between production and decay. For more details on this calculation, please see Ref. [48].
It is possible to study the effects of anomalous couplings of the Higgs boson to the top quark and
bosons. These are
parametrized by
and respectively,
so that in
the SM. Different couplings may be chosen by modifying the variables cttH and cWWH in the
anom_higgs section of the input file.
13.90 and production, processes 560–569
These processes describe the production of a single top quark (or antiquark) by exchange in the -channel, in association with a boson. Processes 560, 561, 564, 567 can be performed at NLO. Processes 560-563 are for stable top quarks, whereas processes 564-569 include the decay of the top quark and antiquark in the approximation inwhich the top quark is taken to be on shell allowing a clean separation between production and decay. For more details on this calculation, please see Ref. [48].
For processes 564 and 567 the default behaviour is that the hadronic decay products are clustered into jets using the supplied jet algorithm parameters, but no cut is applied on the number of jets. This behaviour can be altered by changing the value of the variable notag in the file src/User/setnotag.f.
13.91 production, processes 601–602
These processes represent the production of a pair of Higgs bosons. The production proceeds through gluon-fusion one-loop diagrams involving loops of top quarks. The formulae implemented in the code are taken from ref. [49], where the two Higgs bosons are treated as being on-shell. To enforce this condition, the code sets zerowidth to true, overriding the value set in the input file. The calculation can be performed at LO only, (i.e. one-loop order only). Two decays of the Higgs bosons are currently foreseen, although other decays can easily be implemented. In process 601, one Higgs boson decays to a pair of -quarks, and the other decays to a pair of ’s. In process 602, one Higgs boson decays to a pair of -quarks, and the other decays to a pair of photons.
13.92 production, process 609
This process represents the production of and bosons in association with a jet, with the subsequent decay . Both charges of the boson are summed over and, as a result, the decay products of the boson, particles 3 and 4, represent lepton and antilepton respectively (i.e. they do not correspond to a neutrino and charged lepton). It is primarily of interest as a component part of the NNLO contributions to production. For further information see ref. [22]. This process is calculable at leading LO and next-to-leading order NLO.
13.93 Associated production of and a jet, processes 610-618
These processes represent the production of and bosons in association with a jet, with various decays of the Higgs boson provided. They are primarily of interest as a component part of the NNLO contributions to production. For further information see ref. [22]. This process is calculable at leading LO and next-to-leading order NLO.
13.94 Associated production of and a jet, processes 620-623
These processes represent the production of and bosons in association with a jet, with various decays of the Higgs boson provided. They are primarily of interest as a component part of the NNLO contributions to production. For further information see ref. [22]. This process is calculable at leading LO and next-to-leading order NLO.
13.95 production, processes 640–667
These processes represent the production of a Higgs boson in association with a pair of top quarks. The calculation can be performed at LO only.
For process 640, neither the top quarks nor the Higgs boson decays. In processes 641-647, the top quarks are always produced on-shell, which is a necessity for a gauge invariant result from this limited set of diagrams. Switching zerowidth from .true. to .false. only affects the Higgs and the bosons from the top quark decay. In process 641 both the top quarks decay leptonically and the Higgs boson decays into a pair of bottom quarks. Consistency with the simpler process (640) can be demonstrated by running process 641 with removebr set to true. In process 644 the top quark decays leptonically and the anti-top quark decays hadronically and the Higgs boson decays into a pair of bottom quarks. In process 647 the anti-top quark decays leptonically and the top quark decays hadronically and the Higgs boson decays into a pair of bottom quarks.
Processes 651–657 correspond to processes 641–647 but with the Higgs decaying to two photons. Processes 661–667 correspond to processes 641–647 but with the Higgs decaying to two -bosons which subsequently decay leptonically.